木质素热解生物油组成成分与分子尺寸分布特性分析

引用本文

钟文锐, 刘慧利, 刘欢, 胡建杭. 木质素热解生物油组成成分与分子尺寸分布特性分析[J]. 分子催化, 2023, 37(2): 151-163.

ZHONG Wen-rui, LIU Hui-li, LIU Huan, HU Jian-hang. Characterization of the Composition and Molecular Size Distribution of Lignin Pyrolysis Bio-oil[J]. Journal of Molecular Catalysis (China), 2023, 37(2): 151-163.

基金项目

云南省应用基础研究计划项目(202101AT070135); 国家自然科学基金(U1602272)

作者简介

钟文锐(1997-), 男, 硕士研究生, 从事生物质能利用研究

通讯联系人

刘慧利, E-mail：lhlqwer@163.com

文章历史

收稿日期：2022-11-21
修回日期：2023-01-09

Contents Abstract Full text Figures/Tables PDF

木质素热解生物油组成成分与分子尺寸分布特性分析

钟文锐¹ , 刘慧利¹ , 刘欢¹ , 胡建杭^1,2

1. 昆明理工大学冶金节能减排教育部工程研究中心, 云南昆明 650093;
2. 昆明理工大学省部共建复杂有色金属资源清洁利用国家重点实验室, 云南昆明 650093

收稿日期：2022-11-21；修回日期：2023-01-09

基金项目：云南省应用基础研究计划项目(202101AT070135); 国家自然科学基金(U1602272)

作者简介：钟文锐(1997-), 男, 硕士研究生, 从事生物质能利用研究.

通讯联系人：刘慧利, E-mail：lhlqwer@163.com.

摘要：选用脱碱木质素作为原料, 以热裂解气质联用技术(Py-GC/MS)研究木质素在350~600 ℃下热解产物成分和含量, 并利用Joback法、Lijie法和Tahami法3种基团贡献法计算了生物油各组成成分的临界参数和动力学直径, 对木质素热解油产物的分子动力学直径分布特性进行计算. 结果显示, 愈创木基结构、紫丁香基结构、苯酚类、邻苯二酚类和芳烃类等5种芳香族化合物是350~600 ℃下木质素热解生物油的主要组成成分, 其中愈创木基结构化合物的平均峰面积百分比达到70.7%. 随着反应温度从350提高到600 ℃, 分子动力学直径在0.560~ 0.610 nm区间内的木质素热解油组分含量从14.6%增加至31.3%. 木质素热解生物油主要产物的动力学直径在0.560~0.710 nm, 表明一些孔径尺寸在此范围内的分子筛如SSZ-20、ZSM-5和Beta可作为木质素裂解制备高品质芳烃燃料的催化剂.

关键词：动力学直径木质素择形催化生物油

Characterization of the Composition and Molecular Size Distribution of Lignin Pyrolysis Bio-oil

ZHONG Wen-rui¹ , LIU Hui-li¹ , LIU Huan¹ , HU Jian-hang^1,2

1. Engineering Research Center of Metallurgical Energy Conservation & Emission Reduction, Ministry of Education, Kunming University of Science and Technology, Kunming 650093, China;
2. State Key Laboratory of Complex Nonferrous Metal Resources Clean Utilization, Kunming University of Science and Technology, Kunming 650093, China

Basic Research Foundation of Yunnan Province, China (202101AT070135); The National Natural Science Foundation, China (U1602272)

Author: Zhong Wen-rui (1997-), male, master student, Research Subject: Investigation of biomass energy utilization.

Abstract: The composition and content of lignin pyrolysis bio-oil were analyzed by Pyrolysis-Gas Chromatography/Mass Spectrometry (Py-GC/MS). The critical parameters and kinetic diameters of each constituent of the bio-oil were calculated by Joback method, Lijie method and Tahami method, and the molecular size distribution characteristics of each constituent of the lignin pyrolysis bio-oil were analyzed. The results showed that most of the components of lignin pyrolysis bio-oil were guaiaol-type compounds, syringol-type compounds, phenols, catechols and aromatics in the temperature range from 350 to 600 ℃. The average peak area percentage of the guaiaol-type compounds reached 70.67%. The kinetic diameter of lignin pyrolysis bio-oil components were mostly distributed at [0.560, 0.710)nm. As the reaction temperature rose from 350 to 600 ℃, the percentage of peak area of each bio-oil components in the kinetic diameters range of [0.560, 0.610) nm increased from 14.62% to 31.34%. Zeolite catalysts with pore sizes in the range of 0.560 to 0.710 nm, such as SSZ-20, ZSM-5 and Beta, can be used for lignin catalysis pyrolysis to prepare high-quality aromatic fuels.

Key words: kinetic diameter shape selective catalysis lignin bio-oil

生物质是一种清洁的可再生能源, 具有储量大、分布广泛等优点, 可转化为常规的气体、液体及固体燃料. 生物质热解得到的生物油具备代替汽油、柴油等化石燃料的潜力, 生物质热解制备高品质液体燃料技术受到国内外的广泛关注^[1-2]. 木质纤维素生物质主要由纤维素、半纤维素和木质素3种组分构成. 其中木质素是制浆造纸行业的主要副产物, 来源广泛且价格低廉. 木质素是仅次于纤维素的第二丰富的天然高分子化合物, 目前木质素的主要利用方式是直接燃烧发电, 容易造成资源浪费和环境污染, 如何实现木质素的高效资源化利用是一个重要课题. 木质素是最大的可再生芳烃来源, 是最具前途的制备生物油的可再生原料^[3]. 催化裂解木质素制备高品质芳烃燃料是木质素高效资源化利用的有效方式.

木质素直接热解产生的生物油存在含氧量高、水分高、热值低和酸性强等缺点, 不能直接作为燃料使用. 采用催化裂解的方式可实现木质素热解生物油的脱氧提质, 提高生物油品质, 获得高品质芳烃燃料. 分子筛催化剂是生物油催化裂解提质最常用的催化剂. 分子筛催化剂外表面积占比很小, 远小于内表面积^[4]. 分子筛催化剂的内表面积远大于外表面积, 因此分子筛催化生物油裂解的反应主要发生在分子筛催化剂内部孔道. 需要分子筛孔径略大于生物油分子尺寸, 生物油分子才能自由通过分子筛孔道, 从而生产更多烃类产物, 提高生物油的品质^{[1, 5-6]}. 因此, 有必要研究木质素热解生物油的分子尺寸分布规律, 为分子筛择形催化和木质素热解生物油的催化裂解提供指导.

表征分子尺寸的方式有很多种, 其中以分子动力学直径σ表示分子尺寸由Kington等^[7]首先提出, 使分子尺寸的计算结果与实验值更加吻合. 分子动力学直径σ是Lennard-Jones函数中的关键参数, 是动能无限接近于零的两个分子碰撞时所能达到的最小距离^[8]. 通过分析仪器检测可以获得分子筛的孔径尺寸, 而生物油各组成成分的动力学直径数据却难以获得. 目前仅H₂、H₂O、CO₂等简单分子的动力学直径已通过实验测得, 因实验测量难度极大, 大多数化合物的动力学直径无法通过实验直接获得. 若采用量子化学的方法计算动力学直径, 其计算过程对于木质素热解生物油中4-羟基-3-甲氧基苯乙酮、2-甲氧基-4-丙基苯酚和4-丙烯基-2-甲氧基苯酚等分子质量较大的化合物较为复杂^[9]. 以化合物的临界参数为基础, 通过动力学直径计算模型获得化合物动力学直径的方法计算量少、结果可靠, 是获得木质素热解生物油各组成成分动力学直径数据的有效方式, 而且适用于大分子化合物的计算. 大多数化合物的临界参数难以通过实验测量得到, 学者们常以基团贡献法进行估算^[9-12].

木质素是造纸黑液的主要成分, 催化裂解制备高品质液体燃料是造纸黑液木质素资源化利用的有效手段. 我们以脱碱木质素为研究对象, 研究木质素快速热解生物油各组成成分和含量, 计算生物油各组成成分的临界参数和动力学直径并进行误差分析, 获得生物油各组成成分的动力学直径分布特性和规律, 为分子筛催化造纸黑液木质素热解制备高品质液体燃料过程中分子筛催化剂的选取和催化剂的结构设计提供依据.

1 实验与计算方法 1.1 实验原料

生物质原料为脱碱木质素, 来自广东翁江化学试剂有限公司. 脱碱木质素样品实验前置于65 ℃干燥箱中干燥12 h. 脱碱木质素样品的工业分析和元素分析结果见表 1, 灰分的AAEM元素含量分析见表 2.

表 1 脱碱木质素的工业分析与元素分析 Table 1 Ultimate and proximate analysis of the Lignin (Dealkaline)

表 2 脱碱木质素灰分的AAEM元素含量分析 Table 2 Analysis of AAEM species in ash of Lignin (Dealkaline)

1.2 实验仪器与方法

采用CDS5200热裂解仪(美国CDS Analytical公司)在氦气气氛下对脱碱木质素进行热解, 以1 000 ℃/min的升温速率从室温分别升至350、400、450、500、550和600 ℃, 并维持20 s, 使样品完全裂解. 采用Perkin-Elmer Clarus680GC-SQ8MS型气相色谱-质谱联用仪(GC/MS, 美国Perkinelmer公司)分析热裂解产物, 载气为氦气, 色谱柱为HP-5. 色谱柱升温程序: 进样口温度280 ℃, 在40 ℃保持3 min, 然后以10 ℃/min的升温速率从40升至280 ℃, 并在280 ℃维持5 min, 质谱条件: 电子轰击能量70 eV; 质谱扫描范围40°~350°; EI源温度为250 ℃; 采用NIST 2011标准谱库对质谱图进行检索.

1.3 分子尺寸计算方法

木质素热解油各组成成分的分子尺寸采用Bird等^[8]提出的动力学直径计算模型研究. Bird动力学直径计算模型见式(1)和式(2):

$ \sigma=0.244\left(T_{\mathrm{c}} / 10 P_{\mathrm{c}}\right)^{1 / 3} $

(1)

$ \sigma=0.0841 {V_c}^{1 / 3} $

(2)

式中, σ为动力学直径(nm), V_c、T_c、P_c分别为临界体积(cm³/mol)、临界温度(℃)和临界压力(MPa).

用于估算化合物临界参数的基团贡献法包括一阶基团贡献法、二阶基团贡献法和基于元素、化学键贡献进行估算的方法. Ambrose法^[13-14]、Joback法^[15]、Constantinou/Gani法^[16]和Liang/Ma法^[17]等是应用广泛的一阶基团贡献法, 其中的Joback法估算精度更高、计算简便. Tahami法^[18]是一种二阶基团贡献法, 使用二阶官能团, 不仅提高估算精度还能区分同分异构体. Lijie法^[19]是一种以元素和化学键为基本单元进行估算的基团贡献法, 该方法以新定义的元素和化学键基团进行计算, 计算精度提高. 我们分别采用Joback法、Lijie法和Tahami法3种不同方法对木质素热解生物油各组成成分的临界参数进行计算. 计算方法如下.

1.3.1 Joback基团贡献法计算临界参数

Joback基团贡献法关联式见式(3)-(5).

$ T_c=T_b\left[0.584+0.965 \sum {\mathit{\Delta}} T_i-\left(\sum {\mathit{\Delta}} T_i\right)^2\right]^{-1} $

(3)

$ P_c=0.095\;69\left(0.113+0.003\;2 n_A-\sum {\mathit{\Delta}} P_i\right)^{-2} $

(4)

$ V_c=17.5+\sum n_i {\mathit{\Delta}} V_i $

(5)

式中, P_c、V_c、T_c分别为临界压力(MPa)、临界体积(cm³/mol)和临界温度(℃), T_b为化合物的正常沸点(℃), ΔT_i为第i个基团对临界温度的基团贡献值, n_A为化合物分子中的原子总数, ΔP_i为第i个基团对临界压力的基团贡献值, n_i为化合物分子中所含第i个基团的个数, ΔV_i为第i个基团对临界体积的基团贡献值. Joback基团贡献法中T_c、P_c、V_c 3个临界参数的基团贡献值见表 3. 括号内的数字代表化学键个数.

表 3 Joback法基团贡献值^[15] Table 3 Group contribution paramenters of Joback's group adding method^[15]

Group	ΔP_i	ΔV_i	ΔT_i
Oxygen increments
AOH(1) (phenol)	0.018 4	25	0.024 0
OH (1)(alcohol)	0.011 2	28	0.074 1
O(2) (ring)	0.004 8	13	0.009 8
O(2)	0.001 5	18	0.016 8
C=O(2)	0.003 1	62	0.038 0
C=O(2) (ring)	0.002 8	55	0.028 4
COO(2) (ester)	0.000 5	82	0.048 1
COOH(1) (acid)	0.007 7	89	0.079 1
O=CH(1)(aldehyde)	0.003 0	82	0.037 9
Non-ring increments
C(4)	0.004 3	27	0.006 7
CH(3)	0.002 0	41	0.016 4
CH₂(2)	0.000 0	56	0.018 9
CH₃(1)	-0.001 2	65	0.014 1
=C=(2)	0.002 8	36	0.002 6
=C(3)	0.001 1	38	0.011 7
=CH₂(1)	-0.002 8	56	0.011 3
=CH(2)	-0.000 6	46	0.012 9
Ring increments
=C(3)	0.000 8	32	0.014 3
=CH(2)	0.001 1	41	0.008 2
C(4)	0.006 1	27	0.004 2
CH(3)	0.000 4	38	0.012 2
CH₂(2)	0.002 5	48	0.010 0

表 3 Joback法基团贡献值^[15] Table 3 Group contribution paramenters of Joback's group adding method^[15]

1.3.2 Lijie基团贡献法计算临界参数

Lijie基团贡献法关联式见式(6)-(8).

$ T_c=T_b\left(\mathrm{a}+\sum n_i {\mathit{\Delta}} T_i\right)+\mathrm{b} $

(6)

$ P_c=M\left(\mathrm{a}+\sum n_i {\mathit{\Delta}} P_i\right)^{-2} $

(7)

$ V_c=\mathrm{a}+\mathrm{b} \cdot M+\sum n_i {\mathit{\Delta}} V_i $

(8)

式中, T_b为化合物的正常沸点(℃), n_i为第i个基团的个数, ΔT_i、ΔP_i、ΔV_i为临界参数基团贡献值, M为分子的摩尔质量(g/mol), a和b为方程的系数. Lijie法基团贡献值见表 4, 系数a、b的值见表 5.

表 4 Lijie法基团贡献值^[19] Table 4 Group contribution paramenters of Lijie's group adding method^[19]

表 5 方程参数^[19] Table 5 Constant values of equations^[19]

1.3.3 Tahami基团贡献法计算临界参数

Tahami基团贡献法计算临界温度的关联式见式(9)-(12).

$ T_c=C\left[\ln \left(S_{{\mathit{T1}}}+S_{{\mathit{T2}}}\left(\sum\limits_i N_i T_{c i}\right)+\left(\sum\limits_i N_i T_{c i}\right)^2+\left(\sum\limits_j N_j T_{c j}\right)^2\right)\right] $

(9)

$ C=a+b T_b+c T_b^2+d T_b^3 $

(10)

$ S_{{\mathit{T1}}}=\sum\limits_{\mathrm{k}=1}^{N_A} S_{{\mathit{T1K}}}+\ln \left(n_A\right) $

(11)

$ S_{{\mathit{T2}}}=\sum\limits_{\mathrm{k}=1}^{N_A} S_{{\mathit{T2K}}}+\ln \left(n_A\right) $

(12)

式中, T_c的单位为℃, N_i为第i个一阶基团的个数, N_j为第j个二阶基团的个数, T_ci与T_cj分别为临界温度的一阶和二阶基团贡献值, 见表 6、表 7. T_b是化合物的正常沸点. a、b、c、d是与沸点相关的可调参数, 其值见表 8. S_T1k和S_T2k是关于T_c的可调参数, 与存在的元素种类相关, 与原子数量无关, 其值见表 9. N_A是基团种类的数量. n_A是分子的原子数量.

表 6 Tahami法一阶基团贡献值^[18] Table 6 First order groups and their contributions for critical properties of Tahami method^[18]

Group i	T_ci	P_ci	V_ci
01 CH₃(1)	0.114 78	0.040 23	72.568 18
02 CH₂(2)	0.318 88	0.025 10	49.199 39
03 CH(3)	0.691 54	0.015 57	30.298 66
04 C(4)	0.706 99	0.016 04	16.068 52
05 CH₂(Cycloalkanes)(2)	-0.100 66	0.021 20	43.158 60
06 CH(Cycloalkanes)(3)	0.144 57	0.017 76	33.802 41
07 C(Cycloalkanes)(4)	0.252 46	0.002 46	25.567 58
08 =C(Cycloalkanes)(3)	4.06E-07	0.015 10	0.000 00
09 =CH₂(1)	0.007 59	0.038 10	63.396 51
10 =CH(2)	0.241 03	0.018 85	39.010 29
11 =C(3)	0.424 40	0.012 43	18.373 09
12 =C=(2)	0.009 59	0.000 60	62.196 24
13 =CH(benzene ring)(2)	0.031 33	0.016 97	36.525 93
14 =C(benzene ring)(3)	0.167 45	0.007 90	23.627 56
15 OH(1)(alcohol)	-0.476 01	0.005 97	37.773 16
16 AOH(1)(phenol)	-0.194 00	-0.007 30	18.808 64
17 O(2)(ether)	0.029 98	0.010 36	22.012 13
18 O(2)(Cycloalkanes) (ether)	-0.177 25	0.012 49	22.194 00
19 C=O(Cycloalkanes)(2)(ketone)	17.908 09	0.027 89	57.633 43
20 C=O(2)(ketone)	-0.370 93	0.021 13	53.060 51
21 CH=O(1)(aldehyde)	-1.124 30	0.016 15	67.441 05
22 COOH(1)(acid)	8.41E-08	0.039 81	91.474 86
23 HCOO(1)(formate)	13.329 49	0.037 35	87.566 84
24 COO(2)(ester)	0.505 22	0.035 31	71.185 02
25 =O(1)	-1.376 83	0.027 41	21.571 38

表 6 Tahami法一阶基团贡献值^[18] Table 6 First order groups and their contributions for critical properties of Tahami method^[18]

表 7 Tahami法二阶基团贡献值^[18] Table 7 Second order groups and their contributions for critical properties of Tahami method^[18]

Group j		T_cj	P_cj	V_cj
1	CH₂=CH-	-0.261 11	-0.110 55	0.109 87
2	CH₂=C<	0.897 23	-1.39E-9	-3.42E-04
3	CH₃-CH=	-0.071 39	-0.021 64	0.061 17
4	CH₃-CH₂-CH=	-2.46E-05	-0.062 09	0.200 63
5	CH₃(C-)=	0.569 58	-0.097 74	-0.162 36
6	CH₃-O-	1.061 53	-0.220 68	-0.471 72
7	CH_a-aε(0-3)	0.936 84	-0.076 99	0.013 78
8	Ring	-2.476 98	0.001 69	1.919 09
9	C-C	0.782 75	-0.133 19	-2.923 98
10	C=C	-0.066 10	-0.120 99	-2.998 53
11	Double bone	0.984 22	0.032 60	0.400 50
12	Triple bone	-0.800 45	-0.446 34	7.538 06
13	Cis-	-0.592 52	-0.035 96	10.369 90
14	Trans-	-2.273 26	0.081 08	4.700 83
15	Alpha	0.742 21	-0.035 56	-5.353 01
16	Beta	1.275 63	-2.28E-05	0.672 41
17	C₁ ring	-0.352 33	9.60E-09	-0.844 26
18	C₂ ring	-0.098 90	-0.001 34	-0.776 29
19	C₃ ring	0.000 23	0.098 27	-0.590 09
20	C₄ ring	0.043 77	0.049 67	-0.186 95
21	C₅ ring	0.543 99	0.087 77	-0.642 29
22	C₆ ring	-0.571 29	-0.076 91	1.556 65
23	C₁=C₂	-0.625 25	0.189 90	-0.392 71
24	C₂=C₃	4.233 15	0.170 96	-1.499 21
25	C₃=C₄	-1.972 07	-0.105 89	0.056 51
26	C₄=C₅	-6.306 81	3.05E-13	3.344 88
27	C₅=C₆	-0.533 29	-1.17E-12	0.687 59
28	C₆=C₁	-0.749 53	-0.148 31	-1.405 07
29	Left ring side chain	6.198 45	0.000 13	1.274 38
30	Right ring side chain	-4.709 48	5.56E-09	-0.465 74
31	Middle ring side chain	0.048 72	-0.205 86	0.617 14
32	Oxygen	-0.357 77	1.9E-15	0.384 93

表 7 Tahami法二阶基团贡献值^[18] Table 7 Second order groups and their contributions for critical properties of Tahami method^[18]

表 8-1 可调参数^[18] Table 8-1 Adjustable parameters^[18]

表 8-2 可调参数^[18] Table 8-2 Adjustable parameters^[18]

表 9 元素参数^[18] Table 9 Parameters for atoms^[18]

计算临界压力的关联式见式(13)-(19).

$ \begin{array}{l} P_c=0.1 C\left[\left(S_{{\mathit{P1}}}+S_{{\mathit{P2}}}\left(\sum N_i P_{c i}\right)+\left(\sum N_i P_{c i}\right)^2\right)^{-1}+\left(S_{{\mathit{P3}}}+\right.\right.\\ \left.\left.S_{{\mathit{P4}}}\left(\sum N_j P_{c j}\right)+\left(\sum N_j T_{c j}\right)^2\right)^{-1}+S_{{\mathit{P5}}}\right] \end{array} $

(13)

$ C=\frac{\exp \left(a_1+b_1 T_{\mathrm{b}}\right)}{a_2+b_2 M} $

(14)

$ S_{{\mathit{P1}}}=\sum\limits_{{\rm{k=1}}}^{N_A} S_{{\mathit{P1K}}} $

(15)

$ S_{{\mathit{P2}}}=\sum\limits_{{\rm{k=1}}}^{N_A} S_{{\mathit{P2K}}} $

(16)

$ S_{{\mathit{P3}}}=\sum\limits_{{\rm{k=1}}}^{N_A} S_{{\mathit{P3K}}} $

(17)

$ S_{ P4}=\sum\limits_{{\rm{k=1}}}^{N_A} S_{{\mathit{P4K}}} $

(18)

$ S_{{\mathit{P5}}}=\sum\limits_{{\rm{k=1}}}^{N_A} S_{{\mathit{P5K}}} $

(19)

式中, P_c的单位为MPa, P_ci与P_cj分别为临界压力的一阶和二阶基团贡献值, 见表 6、表 7. M为化合物的分子量. S_P1、S_P2、S_P3、S_P4和S_P5是关于P_c的可调参数, 其值见表 9. a₁、b₁是与沸点相关的可调参数, a₂、b₂是与分子量相关的可调参数, 其值见表 8.

计算临界体积的关联式见式(20)-(22).

$ V_c=\sum\limits_i N_i V_{c i}+\left(S_{{\mathit{V1}}}+\sum\limits_j N_j P_{c j}\right) n_A+S_{{\mathit{V2}}} n_A^2 $

(20)

$ S_{{\mathit{V1}}}=\sum\limits_{{{\rm{k=1}}}}^{N_4} S_{{\mathit{V1K}}} $

(21)

$ S_{{\mathit{V2}}}=\sum\limits_{{{\rm{k=1}}}} S_{{\mathit{V2K}}} $

(22)

式中, V_c的单位为cm³·mol^-1, V_ci与V_cj分别为临界体积的一阶和二阶基团贡献值, 见表 6和表 7. S_V1和S_V2是关于V_c的可调参数, 其值见表 9.

2 结果与讨论 2.1 木质素热解生物油的GC/MS分析

木质素在350~600 ℃温度下的Py-GC/MS分析结果见表 10. 由表可知, 木质素在350~600 ℃下快速热解得到的生物油含有34种化合物, 其主要成分为含甲氧基和酚羟基的芳香族化合物, 还有少量的酸类、酯类、醇类、醚类和酮类化合物. 生物油中愈创木酚、香兰素、2-甲氧基-4-乙烯基苯酚和4-羟基-3-甲氧基苯乙酮等化合物含量较高, 350 ℃时峰面积百分比分别为11.0%、10.4%、10.2%和8.6%, 上述几种化合物分子中均含有甲氧基结构, 是木质素分子结构中C－C键、C－O－C键断裂后的特征产物. 随热解温度升高, 愈创木酚的峰面积百分比从350 ℃时的11.0%增加到600 ℃时的19.8%, 香兰素的峰面积百分比在500 ℃时达到最高为14.4%. 生物油中4-羟基-3-甲氧基苯乙酮、高香草酸、4-丙烯基-2-甲氧基苯酚、2-甲氧基-4-乙烯基苯酚和脱氢枞酸甲酯等分子量较大的化合物峰面积百分比随温度升高而降低. 与文献[20]中报道的两种木质素Py-GC/MS结果进行比较, 都含有愈创木酚、2-甲氧基-4-甲基苯酚和香兰素等主要成分, 且含量随热解温度的变化规律相似.

表 10 木质素在350~600 ℃温度下Py-GC/MS分析结果 Table 10 Components of the components of lignin pyrolysis bio-oil

Chemical composition		Formula	350 ℃	400 ℃	450 ℃	500 ℃	550 ℃	600 ℃
1	Acetic acid	C₂H₄O₂	2.9%	1.7%	1.3%	0.7%	0.6%	-
2	Methyl (R)-(+)-lactate	C₄H₈O₃	2.1%	0.9%	1.0%	0.4%	-	-
3	(R)-propane-1, 2-diol	C₃H₈O₂	1.9%	1.3%	1.2%	1.1%	0.8%	-
4	2-Hydroxy-4-butanolide	C₄H₆O₃	3.2%	1.4%	-	-	-	-
5	Guaiacol	C₇H₈O₂	11.0%	12.6%	13.4%	14.3%	17.2%	19.8%
6	2-Methoxy-4-methylphenol	C₈H₁₀O₂	6.5%	9.1%	10.1%	10.7%	11.6%	12.7%
7	4-Ethyl-2-methoxyphenol	C₉H₁₂O₂	4.5%	5.4%	5.6%	5.9%	6.5%	7.0%
8	2-Methoxy-4-vinylphenol	C₉H₁₀O₂	10.2%	9.1%	8.6%	7.3%	5.5%	1.5%
9	2, 6-Dimethoxyphenol	C₈H₁₀O₃	5.3%	5.4%	7.0%	7.2%	5.8%	5.0%
10	2-Methoxy-4-propylphenol	C₁₀H₁₂O₂	1.1%	2.2%	1.9 %	1.6%	1.9%	1.4%
11	Isoeugenol	C₁₀H₁₂O₂	8.6%	7.7%	7.3%	7.1%	7.0%	6.7%
12	Vanillin	C₈H₈O₃	10.4%	11.4%	12.9%	14.4%	12.0%	8.9%
13	Apocynin	C₉H₁₀O₃	8.6%	4.4%	3.3%	3.0%	4.0%	4.6%
14	Methyl vanillate	C₉H₁₀O4	2.3%	1.8%	1.5%	-	-	-
15	Vanillyl methyl ketone	C₁₀H₁₂O₃	4.9%	3.0%	2.3%	2.1%	2.2%	2.2%
16	Homovanillic acid	C₉H₁₀O4	7.1%	5.3%	3.2%	2.9%	3.0%	2.3%
17	Syringaldehyde	C₉H₁₀O4	2.1%	3.6%	3.7%	4.1%	4.1%	3.9%
18	Methyl dehydroabietate	C₂₁H₃₀O₂	1.3%	0.9%	0.8%	0.7%	-	-
19	Methyl acetate	C₃H₆O₂	-	1.7%	2.0%	1.9%	2.2%	2.7%
20	1, 2-Dimethoxybenzene	C₈H₁₀O₂	-	2.8%	2.0%	1.9%	1.9%	2.2%
21	1, 2-Dimethoxy-4-methylbenzene	C₉H₁₂O₂	-	3.4%	2.9%	2.6%	3.0%	3.1%
22	3, 4-Dimethoxypropiophenone	C₁₀H₁₂O₃	1.4%	1.2%	0.9%	0.8%	0.7%	0.7%
23	L-Lactic acid	C₃H₆O₃	-	-	0.7%	1.2%	0.7%	-
24	4-Methylanisole	C₈H₁₀O	-	-	0.6%	0.5%	-	-
25	3-Methylphenol acetate	C₉H₁₀O₂	3.1%	1.8%	1.3%	-	-	-
26	2, 5-Dimethylphenol	C₈H₁₀O	-	-	1.3%	1.2%	1.4%	1.8%
27	Catechol	C₆H₆O₂	-	-	0.7%	0.9%	1.1%	2.7%
28	Acetol	C₃H₆O₂	-	-	-	0.7%	1.2%	1.4%
29	Toluene	C₇H₈	-	-	0.4%	0.5%	0.8%	1.2%
30	Phenol	C₆H₆O	0.7%	1.1%	1.2%	1.4%	1.7%	2.3%
31	o-Cresol	C₇H₈O	0.9%	1.0%	1.0%	1.2%	1.6%	2.3%
32	4-Methylcatechol	C₇H₈O₂	-	-	-	1.9%	1.2%	0.8%
33	Benzene	C₆H₆	-	-	-	-	0.6%	0.9%
34	Salicylaldehyde	C₇H₆O₂	-	-	-	-	-	2.2%
“-”: Not detected

表 10 木质素在350~600 ℃温度下Py-GC/MS分析结果 Table 10 Components of the components of lignin pyrolysis bio-oil

根据木质素热解生物油各组成成分的结构特征将生物油的主要成分划分为芳烃类(AH)、苯酚类(H)、邻苯二酚类(C)、愈创木基结构(G)和紫丁香基结构(S)5种类型. 各类化合物的峰面积百分比见表 11. 由表可知, 木质素350~600 ℃的快速热解产物主要为愈创木基结构的化合物(G), 平均峰面积百分比达到70.8%. 在350和400 ℃时未检出芳烃类化合物. 随热解温度升高, 苯酚类和芳烃类化合物的峰面积百分比增加, 600 ℃时芳烃类和苯酚类化合物的峰面积百分比分别达到2.1%和8.6%.

表 11 木质素热解产物化合物类别含量统计表 Table 11 Statistics of compound category content of lignin pyrolysis products

2.2 木质素热解生物油各组分的动力学直径

分别采用Joback法、Lijie法和Tahami法计算木质素热解生物油各组成成分的临界参数, 通过式(1)-(2)计算获得生物油各组成成分的动力学直径, 计算结果见表 12. 采用(1)、(2)式计算得到的两组动力学直径分别记为σ₁和σ₂, 平均值记为σ_ave.

表 12 木质素热解生物油动力学尺寸 Table 12 Kinetic diameters of the components of lignin pyrolysis bio-oil

	Chemical composition	Joback method			Lijie method			Tahami method
	Chemical composition	σ₁	σ₂	σ_ave	σ₁	σ₂	σ_ave	σ₁	σ₂	σ_ave
1	Acetic acid	0.532	0.467	0.500	0.502	0.471	0.487	0.522	0.470	0.496
2	Methyl (R)-(+)-lactate	0.577	0.562	0.569	0.589	0.570	0.580	0.593	0.565	0.579
3	(R)-propane-1, 2-diol	0.585	0.519	0.552	0.548	0.520	0.534	0.553	0.522	0.537
4	2-Hydroxy-4-butanolide	0.495	0.537	0.516	0.530	0.544	0.537	0.548	0.538	0.543
5	Guaiacol	0.617	0.595	0.606	0.609	0.599	0.604	0.606	0.588	0.597
6	2-Methoxy-4-methylphenol	0.651	0.625	0.638	0.645	0.628	0.637	0.642	0.624	0.633
7	4-Ethyl-2-methoxyphenol	0.679	0.652	0.665	0.677	0.655	0.666	0.668	0.678	0.673
8	2-Methoxy-4-vinylphenol	0.668	0.610	0.639	0.666	0.652	0.659	0.632	0.648	0.640
9	2, 6-Dimethoxyphenol	0.677	0.634	0.655	0.670	0.640	0.655	0.654	0.654	0.654
10	2-Methoxy-4-propylphenol	0.711	0.648	0.679	0.707	0.680	0.694	0.672	0.705	0.688
11	Isoeugenol	0.701	0.668	0.684	0.702	0.677	0.689	0.694	0.696	0.695
12	Vanillin	0.602	0.633	0.617	0.622	0.638	0.630	0.609	0.648	0.629
13	Apocynin	0.683	0.655	0.669	0.703	0.664	0.683	0.633	0.625	0.629
14	Methyl vanillate	0.691	0.664	0.677	0.704	0.675	0.689	0.687	0.670	0.678
15	Vanillyl methyl ketone	0.698	0.668	0.683	0.728	0.688	0.708	0.707	0.710	0.709
16	Homovanillic acid	0.691	0.663	0.677	0.713	0.674	0.694	0.700	0.696	0.698
17	Syringaldehyde	0.646	0.668	0.657	0.664	0.675	0.669	0.655	0.688	0.671
18	Methyl dehydroabietate	1.014	0.846	0.930	0.936	0.859	0.898	0.946	0.894	0.920
19	Methyl acetate	0.552	0.515	0.534	0.538	0.517	0.527	0.545	0.515	0.530
20	1, 2-Dimethoxybenzene	0.702	0.626	0.664	0.663	0.628	0.646	0.660	0.629	0.645
21	1, 2-Dimethoxy-4-methylbenzene	0.689	0.653	0.671	0.652	0.655	0.654	0.672	0.663	0.667
22	3, 4-Dimethoxypropiophenone	0.766	0.677	0.722	0.743	0.688	0.716	0.727	0.695	0.711
23	L-Lactic acid	0.519	0.523	0.521	0.523	0.534	0.528	0.552	0.570	0.561
24	4-Methylanisole	0.677	0.616	0.647	0.641	0.616	0.629	0.651	0.622	0.637
25	3-Methylphenol acetate	0.706	0.648	0.677	0.664	0.653	0.658	0.690	0.659	0.674
26	2, 5-Dimethylphenol	0.647	0.615	0.631	0.626	0.613	0.620	0.633	0.634	0.633
27	Catechol	0.615	0.560	0.588	0.566	0.566	0.566	0.542	0.547	0.544
28	Acetol	0.543	0.514	0.529	0.541	0.512	0.527	0.549	0.517	0.533
29	Toluene	0.620	0.575	0.597	0.577	0.571	0.574	0.590	0.573	0.581
30	Phenol	0.578	0.550	0.564	0.549	0.555	0.552	0.553	0.536	0.545
31	o-Cresol	0.611	0.584	0.598	0.595	0.585	0.590	0.592	0.575	0.583
32	4-Methylcatechol	0.645	0.594	0.619	0.603	0.599	0.601	0.583	0.582	0.583
33	Benzene	0.586	0.539	0.563	0.531	0.534	0.533	0.549	0.534	0.542
34	Salicylaldehyde	0.586	0.594	0.590	0.597	0.596	0.596	0.567	0.577	0.572

表 12 木质素热解生物油动力学尺寸 Table 12 Kinetic diameters of the components of lignin pyrolysis bio-oil

为验证本研究木质素热解生物油分子尺寸计算结果的可靠性, 采用文献[2, 21-22]报道的数据进行验证. 文献[2, 21]和^[22]报道了乙酸、乙酸甲酯、甲苯、邻甲酚和苯的动力学直径分别为0.440、0.478、0.584、0.654和0.585 nm. 与文献报道的5种化合物的动力学直径数据比较, Joback法、Lijie法和Tahami法的平均误差分别为7.97%、8.28%和8.41%, Joback法在3种计算方法中误差最低, 是最优的基团贡献法. 5种化合物中误差最大的为乙酸, 3种计算方法的误差分别为13.61%、10.56%和12.70%. 误差最小的为甲苯, 3种计算方法的误差分别为2.28%、1.73%和0.46%. Joback法、Lijie法和Tahami法3种方法计算乙酸和乙酸甲酯动力学直径的平均误差分别为12.62%、10.45%和11.78%, 计算甲苯、邻甲酚和苯3种化合物动力学直径的平均误差分别为4.92%、6.84%和6.22%, 3种计算方法用于估算芳香族化合物的动力学直径时误差更低, 而木质素热解生物油的主要组成成分为芳香族化合物, 因此本研究采用的3种方法用于估算木质素热解生物油各组成成分的动力学直径合理, 可靠性较高.

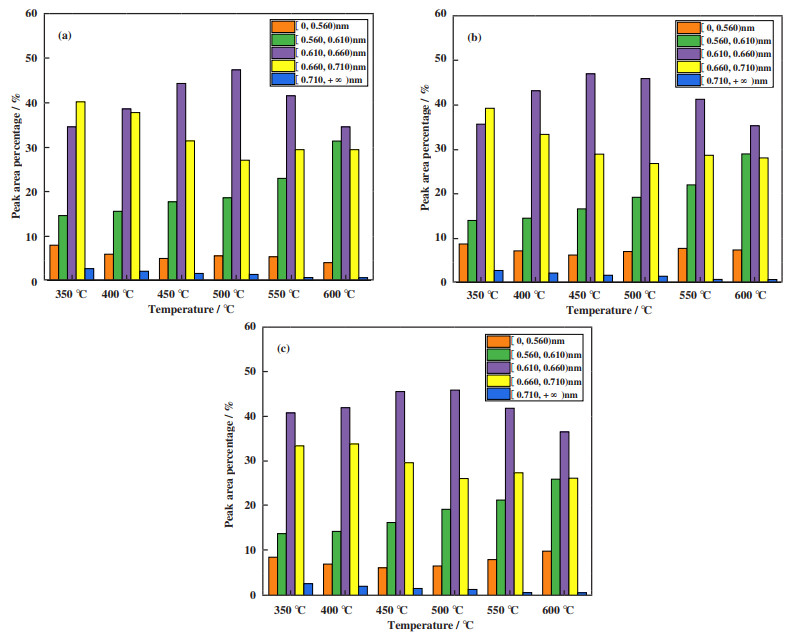
2.3 生物油分子尺寸分布规律

木质素在350~600 ℃温度区间内热解产生生物油各组成成分的动力学直径分布见图 1, 其中图 1(a)、图 1(b)、图 1(c)分别为Joback法、Lijie法和Tahami法的计算结果. 由图 1可知, 采用3种基团贡献法结合动力学直径计算模型获得的生物油各组成成分动力学直径分布差别较小. 由图 1(a)可知, 木质素350 ℃热解生物油各组成成分的动力学直径主要分布在0.560~0.710 nm, 当热解温度由350升高到600 ℃时, 动力学直径分布范围位于0.560~0.610 nm的生物油各组成成分的峰面积百分比由14.6%增加到31.3%, 位于0.610~0.660 nm的生物油各组成成分的峰面积百分比在500 ℃时达到峰值47.3%, 当热解温度升高到600 ℃时峰面积百分比又降至34.5%, 位于0.660~0.710 nm的生物油各组成成分的峰面积百分比在500 ℃时达到最低(27.1%). 图 1(b)与图 1(c)中热解生物油各组成成分动力学直径分布规律与图 1(a)一致. 木质素在350~600 ℃热解产生生物油各组成成分的动力学直径位于0.560~0.710 nm的峰面积百分比均大于85%. 木质素热解生物油催化裂解制备高品质芳烃燃料时, 为提高目标产物的产率, 从分子筛催化剂的孔径与生物油分子尺寸的择形催化的角度考虑, 应优先选用SSZ-20、ZSM-5和Beta等孔径尺寸在0.560~0.720 nm范围内的分子筛催化剂.

图 1 各温度下木质素热解生物油动力学直径分布 Fig.1 Kinetic diameter distribution of bio-oil at different temperatures (a)Joback基团贡献法; (b) Lijie基团贡献法; (c) Tahami基团贡献法 (a) Joback method; (b) Lijie method; (c) Tahami method

3 结论

以脱碱木质素为生物质原料, 研究生物质热解油的组成成分, 进行了生物油分子尺寸分布特性分析, 得出以下结论:

(1) 脱碱木质素热解生物油的成分主要由愈创木基结构、紫丁香基结构、苯酚类、邻苯二酚类和芳烃类5种芳香族化合物构成. 木质素350~600 ℃热解产物以愈创木基结构化合物为主, 平均峰面积百分比达70.7%, 其中愈创木酚和香兰素的峰面积百分比最高, 分别为14.7%和11.7%.

(2) 随热解温度的升高, 木质素热解生物油各组成成分动力学直径位于0.560~0.610 nm区间内的峰面积百分比从350 ℃时的14.6%增加至600 ℃时的31.3%, 位于0.610~0.660 nm的生物油各组成成分的峰面积百分比在500 ℃时达到峰值(47.3%), 位于0.660~0.710 nm的生物油各组成成分的峰面积百分比在500 ℃时达到最低(27.1%).

(3) 木质素在350~600 ℃热解产生生物油各组成成分的动力学直径在0.560~0.710 nm之间的峰面积百分比含量大于85%, 生物油催化裂解制备高品质芳烃燃料适合选用SSZ-20、ZSM-5和Beta等孔径尺寸在0.560~0.710 nm范围内的分子筛催化剂.

参考文献

[1]	a. Foster A J, Jae J, Cheng Y, et al. Optimizing the aromatic yield and distribution from catalytic fast pyrolysis of biomass over ZSM-5[J]. Appl Catal A, 2012, 423/424: 154-161. b. Yang Jian(杨坚), Li Xue-mei(李雪梅), Zhang Jia (张佳), et al. Reductive amination of biomass-derived 2-hydroxytetrahydropyran to 5-amino-1-pentanol over bimetallic Ni-Fe/Al₂O₃ catalysts(Ni-Fe-Al-O双金属催化剂在生物质基2-羟基四氢吡喃还原胺化合成5-氨基-1-戊醇中的性能研究)[J]. J Mol Catal(China)(分子催化), 2022, 36(2): 118-128. c. Wang Zheng(王征), Lin Qing(蔺庆), Zhang Xiang-long(张相龙), et al. Recent progress in homogeneous catalytic hydrogenation of γ- and δ-ketoacid derivatives(γ-和δ-酮酸衍生物均相催化氢化研究进展)[J]. J Mol Catal(China)(分子催化), 2021, 35(2): 178-187.
[2]	Jae J, Tompsett G A, Foster A J, et al. Investigation into the shape selectivity of zeolite catalysts for biomass conversion[J]. J Catal, 2011, 279(2): 257–268. DOI:10.1016/j.jcat.2011.01.019
[3]	a. Li C, Zhao X, Wang A, et al. Catalytic transformation of lignin for the production of chemicals and fuels[J]. Chem Rev, 2015, 115(21): 11559-11624. b. Huang Yu(黄钰), Bao Gui-rong(包桂蓉), Luo Jia(罗嘉), et al. Study on Ce/Cu/Zn/Al catalyzed conversion of lignin to phenols in supercritical methanol(超临界甲醇中Ce/Cu/Zn/Al催化木质素制备酚类化合物的研究)[J]. J Mol Catal(China)(分子催化), 2020, 34(1): 58-64.
[4]	Yu Y, Li X, Su L, et al. The role of shape selectivity in catalytic fast pyrolysis of lignin with zeolite catalysts[J]. Appl Catal A, 2012, 447/448: 115–123. DOI:10.1016/j.apcata.2012.09.012
[5]	Fogassy G, Thegarid N, Schuurman Y, et al. From biomass to bio-gasoline by FCC co-processing: Effect of feed composition and catalyst structure on product quality[J]. Energy Environ Sci, 2011, 4(12): 568–576.
[6]	Paul T W, Nittaya N. Comparison of products from the pyrolysis and catalytic pyrolysis of rice husks[J]. Energy, 2000, 25(6): 493–513. DOI:10.1016/S0360-5442(00)00009-8
[7]	Kington G L, Macleod A C. Heats of sorption of gases in chabazite, energetic heterogeneity and the role of quadrupoles in sorption[J]. Trans Faraday Soc, 1959, 55: 1799–1814. DOI:10.1039/tf9595501799
[8]	Bird R B, Stewart W E, Lightfoot E N. Transport phenomena[M]. New York: John Wiley & Sons Inc, 2002.
[9]	Wang Ya-si(王亚思), Zhang Kai-yin(张开银), Liu Hui-li(刘慧利), et al. Molecular size distribution characteristics of cellulose pyrolysis bio-oil(纤维素热解生物油分子尺寸分布特性)[J]. Chin J Process Eng(过程工程学报), 2021, 21(5): 609-616
[10]	Wang Xiao-yan(王小艳), Si Ji-lin(司继林), Zhang Da(张达), et al. Research progress of estimation methods for critical parameters of pure substances(纯物质临界参数估算方法的研究进展)[J]. Chem Ind Eng Prog(化工进展), 2012, 31(9): 1871-1877.
[11]	Zhang Hong-yan(张红彦), Ma Pei-Sheng(马沛生). The evaluation methods for critical parameter(临界参数的估算方法)[J]. Chem Ind Eng(化学工业与工程), 2000, 2000(3): 149-155.
[12]	Xia Li(夏力), Jin Li-qiang(金力强), Li Zhong-jie(李忠杰), et al. Comparison and evaluation of group-contribution techniques for estimating the normal boiling point of organic compounds(估算有机物正常沸点的基团贡献法比较与评价)[J]. Comput Appl Chem(China)(计算机与应用化学), 2007, 2007(7): 944-948.
[13]	Ambrose D. Correlation and Estimation of Vapour-liquid Critical Properties: Critical pressures and critical volumes of organic compounds[M]. Teddington: National Physical Laboratory, 1979.
[14]	Ambrose D. Correlation and estimation of vapour-liquid critical properties: Critical temperatures of organic compounds[M]. Teddington: National Physical Laboratory, 1978.
[15]	Joback K G, Reid R C. Estimation of pure-component properties from group-contributions[J]. Chem Eng Commun, 1987, 57(1/6): 233–243.
[16]	Constantinou L, Gani R. New group contribution method for estimating properties of pure compounds[J]. Aiche J, 1994, 40(10): 1697–1710. DOI:10.1002/aic.690401011
[17]	Liang Ying-hua, Ma Pei-sheng. A new group-contribution method for critical properties[J]. Chin J Chem Eng, 2000, 8(1): 74–79.
[18]	Tahami S, Movagharnejad K, Ghasemitabar H. Estimation of the critical constants of organic compounds via a new group contribution method[J]. Fluid Phase Equilib, 2019, 494: 45–60. DOI:10.1016/j.fluid.2019.04.022
[19]	Li J, Xia L, Xiang S. A new method based on elements and chemical bonds for organic compounds critical properties estimation[J]. Fluid Phase Equilib, 2016, 417: 1–6. DOI:10.1016/j.fluid.2016.01.008
[20]	Jiang G, Nowakowski D J, Bridgwater A V. Effect of the temperature on the composition of lignin pyrolysis products[J]. Energy Fuels, 2010, 24(8): 4470–4475. DOI:10.1021/ef100363c
[21]	Bowen T C, Noble R D, Falconer J L. Fundamentals and applications of pervaporation through zeolite membranes[J]. J Membr Sci, 2004, 245(1/2): 1–33.
[22]	Wu Jie(武杰). Research on the correlation between dynamic diameters of hydrocarbon molecules and zeolites shape-selective catalytic performance(烃分子动力学直径与分子筛择形催化性能的相关性)[J]. Chem Ind Eng Prog (化工进展), 2016, 35(S1): 167-173.